Alpha blending – Mélanger programmatiquement des couleurs semi-transparentes

La plupart des langages de programmation proposent des outils pour travailler sur des images directement au niveau binaire, soit via une matrice d’octets. Ainsi chaque pixel d’image peut être codé sur 3 octets si le format ne prend pas en compte la transparence (RGB), ou sur 4 octets si le format prend en compte la transparence (RGBA). Dans le cas du RGBA, si l’on souhaite appliquer une couleur partiellement transparentes par-dessus ou en-dessous d’une autre couleur elle-même partiellement transparente, le calcul du nouveau pixel RGBA n’est pas forcément intuitif. Pourtant, des formules existent pour cette opération appelée alpha blending.

Les différents cas possibles

Si nous appliquons une couleur A sur une couleur B (ou une couleur B sous une couleur A, le calcul est le même), selon l’opacité ou la transparence de chacune, on peut distinguer 4 situations :

Deux cas sont évidents : ceux où A est opaque. Dans les deux autres cas, on constate qu’une troisième couleur apparaît, qui est le fruit du mélange des deux autres.

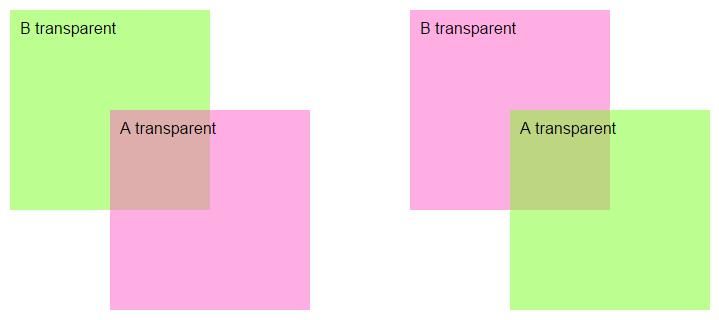
Attention, l’ordre est important : si A et B sont partiellement transparents, la couleur produite par A sur B ne sera pas la même que pour B sur A :

Les formules de Porter et Duff

Les équations de Porter et Duff permettent de calculer la couleur produite dans les différents cas. Si l’on superpose une couleur A sur une couleur B pour produire une couleur C, que l’on appelle Aa, Ba et Ca les transparences de chacune de ces couleurs ramenées à un coefficient entre 0 (totalement transparent) et 1 (opaque), et Argb, Brgb et Crgb leurs composantes RGB, la formule générale est la suivante :

Ca = Aa + Ba * (1 – Aa)

Crgb = (Argb * Aa + Brgb * Ba * (1 – Aa)) / Ca

Dans le cas où B est opaque, la formule est simplifiée en :

Ca = 1

Crgb = Argb * Aa + Brgb * (1 – Aa)

Dans les deux formules, le calcul de Crgb doit être réalisé pour chaque composante (rouge, vert, bleu) avec les valeurs correspondantes dans les couleurs à mélanger.

Exemple d’implémentation : en Java

Nous avons exposé le principe mathématique général. Chaque langage dispose des structures et opérations de base pour implémenter ces formules dans un algorithme de traitement d’image.

Ici, nous étudions le cas de l’application a posteriori d’un background opaque sous une image partiellement transparente. Nous accédons au tableau de bytes représentant l’image via l’objet BufferedImage.

private static void applyBackgroundColor(BufferedImage pBufferedImage, String pColor) {
   // récupération du tableau de bytes
   final byte[] lPixels = ((DataBufferByte) pBufferedImage.getRaster()
      .getDataBuffer()).getData();
   // offset pour le déplacement dans la matrice
   int lOffset = 0;
   // récupération des dimensions de l’image
   final int lWidth = pBufferedImage.getWidth();
   final int lHeight = pBufferedImage.getHeight();
   // initialisation de la couleur de fond à appliquer
   final Color lColor = Color.decode("#" + pColor);
   final double lRed = lColor.getRed();
   final double lGreen = lColor.getGreen();
   final double lBlue = lColor.getBlue();
   // création d’une variable pour stocker le coefficient de transparence
   double lRelativeAlpha;
   // on boucle sur les colonnes et lignes de la matrices
   for (int y = 0; y <
 lHeight; y++) {
      for (int x = 0; x <
 lWidth; x++, lOffset++) {
         // on calcule le coefficient de transparence du pixel courant
         lRelativeAlpha = Integer.valueOf(lPixels[lOffset * 4]&0xFF).doubleValue()/255D;
         // on applique le fond
         // composante bleue
         lPixels[lOffset * 4 + 1] = (byte) Double.valueOf((Integer.valueOf(lPixels[lOffset * 4 + 1]&0xFF).doubleValue()*lRelativeAlpha)
            +(lBlue*(1D-lRelativeAlpha))).intValue();
         // composante verte
         lPixels[lOffset * 4 + 2] = (byte) Double.valueOf((Integer.valueOf(lPixels[lOffset * 4 + 2]&0xFF).doubleValue()*lRelativeAlpha)
            +(lGreen*(1D-lRelativeAlpha))).intValue();
         // composante rouge
         lPixels[lOffset * 4 + 3] = (byte) Double.valueOf((Integer.valueOf(lPixels[lOffset * 4 + 3]&0xFF).doubleValue()*lRelativeAlpha)
            +(lRed*(1D-lRelativeAlpha))).intValue();
         // on applique la nouvelle transparence
         lPixels[lOffset * 4] = -1;
      }
   }
}

Comme vous pouvez le constater, la mise en oeuvre des équations de Porter et Duff n’a rien de sorcier. Une difficulté toutefois, inhérente à la technologie choisie : nous souhaitons travailler sur des valeurs de 0 à 255 donc sur un entier non signé codé sur un octet. Cela n’existe pas en JavaLangage de développement très populaire !, d’où ces opérations verbeuses pour obtenir la valeur entière non signée des bits correspondant à un byte, puis pour travailler sur des relatifs (à cause du coefficient entre 0 et 1), puis pour retomber sur une valeur entière sous forme d’un byte. Toutefois, malgré la verbosité du code, l’opération s’avère tout-à-fait performante.